演講時間：113年11月8日下午1點30分   
演講地點：A813
講題: Conservative Physics-Informed Neural Networks for Non-Conservative Hyperbolic Conservation Laws Near Critical States
摘要:
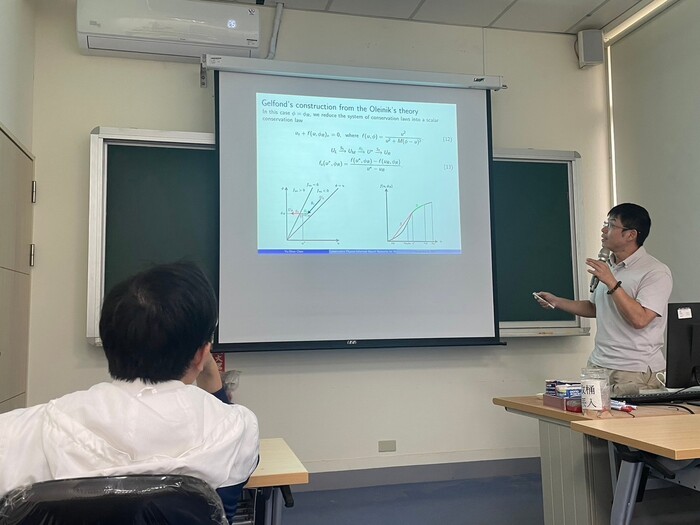
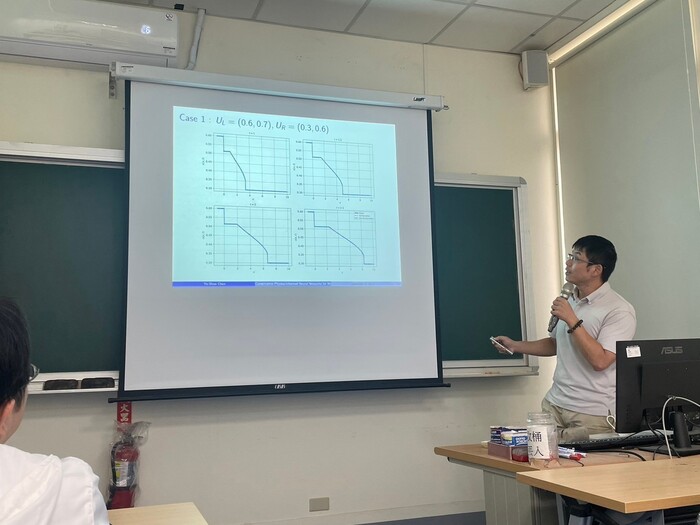
In this talk, a modified version of conservative Physics-informed Neural Networks (cPINN for short) is provided to construct the weak solutions of Riemann problem for the hyperbolic scalar conservation laws in nonconservative form. To demonstrate the results, we use the model of generalized Buckley-Leverett equation (GBL equation for short) with discontinuous porosity in porous media. By inventing a new unknown, the GBL equation is transformed into a two-by-two resonant hyperbolic conservation laws in conservative form. The modified method of cPINN is invented to overcome the difficulties due to the discontinuity of the porosity and the appearance of the critical states (near vacuum) in the Riemann data. We experiment with our idea by using a deep learning algorithm to solve the GBL equation in both conservative and non-conservative forms, as well as the cases of critical and non-critical states. This method provides a combination of two different neural networks and corresponding loss functions, one is for the two-by-two resonant hyperbolic system, and the other is for the scalar conservation law with a discontinuous perturbation term in the non-convex flux. The technique of re-scaling to the unknowns is adopted to avoid the oscillation of the Riemann solutions in the cases of critical Riemann data. The solutions constructed by the modified cPINN match the exact solutions constructed by the theoretical analysis for hyperbolic conservation laws.

活動海報與照片: